Schülerübungen zu Exponentialfunktionen
Teste dein Wissen!
Aufgabe 1: Exponentieller Zerfall der CO₂-Konzentration
Nach einer Unterrichtsstunde liegt die CO₂-Konzentration in einem Klassenraum bei etwa 1600 ppm. Daraufhin wird intensiv gelüftet. Die Konzentration sinkt, da die Raumluft mit Frischluft vermischt wird. Die Außenluft enthält etwa eine CO₂-Konzentration von 400 ppm. Nach 10 Minuten Lüften beträgt die Konzentration im Klassenzimmer nur noch 1000 ppm. Dieser Abbau der CO₂-Konzentration lässt sich näherungsweise mit einer exponentiellen Zerfallsfunktion beschreiben.
Abnahme der CO₂-Konzentration in ppm in Abhängigkeit der Zeit:
Aufgabe 2: CO₂-Zerfall in verschiedenen Lüftungsszenarien
In einem geschlossenen Raum wird nach einer Unterrichtsstunde eine CO₂-Konzentration von 1600 ppm gemessen. Um die Luftqualität zu verbessern, kann der Raum auf drei verschiedene Arten gelüftet werden: durch gekippte Fenster (langsame Lüftung) durch leicht geöffnete Fenster (mittlere Lüftung) und durch eine automatische Lüftungsanlage (schnelle Lüftung).
Die zeitliche Entwicklung der CO₂-Konzentration C(t) (in ppm) in Abhängigkeit von der Zeit t (in Minuten) lässt sich jeweils durch die abgebildeten exponentiellen Funktionen beschreiben.
Aufgabestellung: Ordne den einzelnen Graphen die korrekte Situation zu.
Aufgabe 3: Analyse des CO₂-Zerfalls im Raum
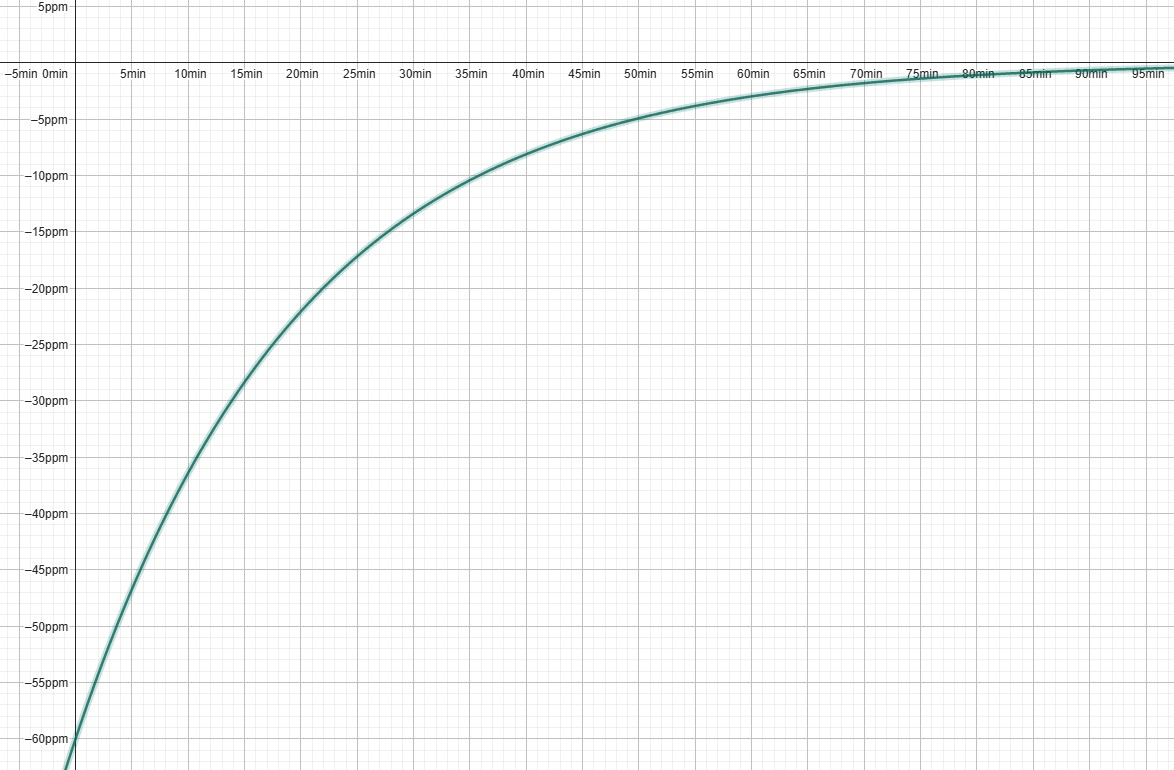
Die Funktion C(t) = 400+1200⋅e−0.05t beschreibt den CO₂-Gehalt (in ppm) in einem Raum, der nach einer Unterrichtsstunde gelüftet wird. Die Außenluftkonzentration beträgt 400 ppm, und die Startkonzentration im Raum beträgt 1600 ppm.
Änderungsrates der Kohlendioxidkonzentration in Abhängigkeit der Zeit:
Aufgabe 4: Exponentielle Zerfallsprozesse
Die Funktion C'(t)=400+1200⋅e−kt beschreibt näherungsweise die CO₂-Konzentration C(t) (in ppm) in Abhängigkeit von der Zeit t (in Minuten) in einem Raum, der gelüftet wird. Dabei ist k > 0 die Zerfallskonstante, die die Lüftungsintensität beschreibt.
Link Materialbeschreibung
- Exponentialfunktion der CO₂-Abnahme
Mithilfe dieser vier interaktiven Übungen im Mathematikunterricht der Sekundarstufe II arbeiten die Schülerinnen und Schüler mit Exponentialfunktionen und untersuchen deren Steigung und Ableitung im Anwendungskontext der Entwicklung der CO₂-Konzentration beim Lüften eines Raumes. Die interaktiven Übungen stehen als Link und als Download zur Verfügung.
