In dieser Unterrichtseinheit setzen sich die Schülerinnen und Schüler mit Exponentialfunktionen im Kontext von Temperatur- und Luftfeuchtigkeitsveränderungen in Innenräumen auseinander. Dabei handelt es sich um ein Thema, welches sie aus ihrem eigenen Alltag kennen. Der Ausgangspunkt ist die alltagsnahe Problemstellung von Kondenswasserbildung in Badezimmern und die Frage, welche Rolle Temperatur, Luftfeuchtigkeit und Belüftungssysteme dabei spielen.
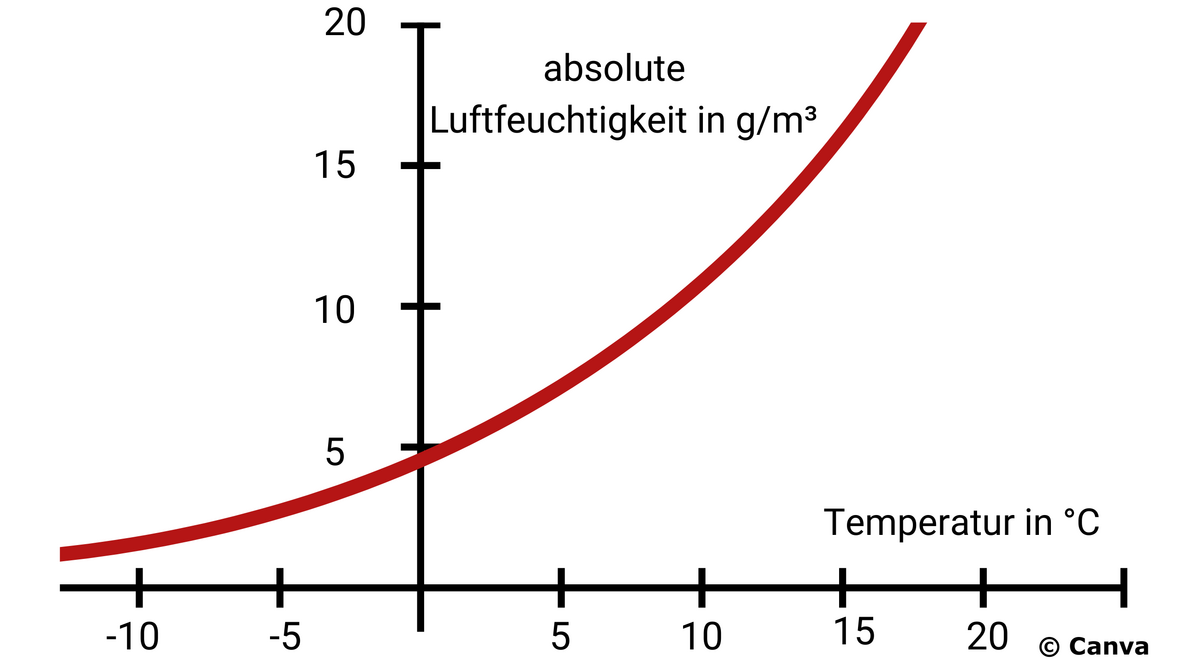
Zu Beginn der Einheit lernen die Schülerinnen und Schüler anhand eines Graphen, der die absolute Luftfeuchtigkeit in Abhängigkeit von der Temperatur zeigt, die charakteristische Form einer Exponentialfunktion kennen. Sie beschreiben den Graphen, lesen Werte ab und übertragen die Erkenntnisse auf eine Funktionsgleichung. Dabei verknüpfen die Lernenden mathematische Konzepte mit einer Problematik, die sie aus dem Alltag kennen – der Feuchtigkeit in Badezimmern. Sprintaufgaben für leistungsstarke und schnelle Schülerinnen und Schüler ermöglichen eine Differenzierung.
Anschließend wird das Taupunktdiagramm eingeführt, das im Bereich Sanitär-, Heizungs- und Klimatechnik (SHK) zur Beurteilung von Feuchtigkeitsproblemen genutzt wird. In einer anschließenden Gruppenarbeitsphase bearbeiten die Lernenden unterschiedliche Textaufgaben zur Luftfeuchtigkeit und untersuchen, wie sich der Startwert einer Exponentialfunktion auf den Graphen auswirkt.
Im weiteren Verlauf beschäftigen sich die Lernenden mit der exponentiellen Abnahme, indem sie eine GeoGebra-Anwendung nutzen, um den Einfluss von Funktionsparametern zu untersuchen. Diese Erkenntnisse werden auf die reale Abkühlung eines Badezimmers nach dem Duschen übertragen – eine Situation, die sie aus ihrem täglichen Leben kennen. In einer komplexen Anwendungsaufgabe berechnen die Lernenden, wie lange ein Lüfter benötigt, um die Luftfeuchtigkeit auf ein bestimmtes Niveau zu senken. Differenzierung erfolgt hier über optionale Hilfestellungen und gestufte Aufgabenformate.
Die Einheit schließt mit einem Rückbezug zur Eingangsfrage: Gemeinsam erarbeiten die Schülerinnen und Schüler konkrete Lüftungsempfehlungen zur Schimmelvermeidung. Durch die kontinuierliche Verknüpfung von mathematischen Inhalten mit vertrauten Alltagssituationen und SHK-relevanten Anwendungen erhalten die Lernenden einen handlungsorientierten Zugang zu exponentiellen Funktionen und lernen, mathematische Konzepte zur Lösung realer Probleme im Handwerk anzuwenden.